
by Valluru B. Rao
M&T Books, IDG Books Worldwide, Inc.
ISBN: 1558515526 Pub Date: 06/01/95

|
C++ Neural Networks and Fuzzy Logic
by Valluru B. Rao M&T Books, IDG Books Worldwide, Inc. ISBN: 1558515526 Pub Date: 06/01/95 |
| Previous | Table of Contents | Next |
Table 5.3 lists the vertices and their coordinates, together with a flag that indicates to which subset in the partitioning the vertex belongs. Note that you can think of the action of the Multilayer Perceptron as that of evaluating the intersection and union of linearly separable subsets.
| Vertex | Coordinates | Subset |
|---|---|---|
| O | (0,0,0) | 1 |
| A | (0,0,1) | 1 |
| B | (0,1,0) | 2 |
| C | (0,1,1) | 2 |
| D | (1,0,0) | 2 |
| E | (1,0,1) | 2 |
| F | (1,1,0) | 3 |
| G | (1,1,1) | 3 |
The network, which is a two-layer Perceptron, meaning two layers of weights, has three neurons in the first layer and one output neuron in the second layer. Remember that we are counting those layers in which the neurons do the aggregation of the signals coming into them using the connection weights. The first layer with the three neurons is what is generally described as the hidden layer, since the second layer is not hidden and is at the extreme right in the layout of the neural network. Table 5.4 gives an example of the weights you can use for the connections between the input neurons and the hidden layer neurons. There are three input neurons, one for each coordinate of the vertex of the cube.
| Input Neuron # | Hidden Layer Neuron # | Connection Weight |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 0.1 |
| 1 | 3 | -1 |
| 2 | 1 | 1 |
| 2 | 2 | -1 |
| 2 | 3 | -1 |
| 3 | 1 | 0.2 |
| 3 | 2 | 0.3 |
| 3 | 3 | 0.6 |
Now we give, in Table 5.5, the weights for the connections between the three hidden-layer neurons and the output neuron.
| Hidden Layer Neuron # | Connection Weight |
|---|---|
| 1 | 0.6 |
| 3 | 0.3 |
| 3 | 0.6 |
It is not apparent whether or not these weights will do the job. To determine the activations of the hidden-layer neurons, you need these weights, and you also need the threshold value at each neuron that does processing. A hidden-layer neuron will fire, that is, will output a 1, if the weighted sum of the signals it receives is greater than the threshold value. If the output neuron fires, the function value is taken as +1, and if it does not fire, the function value is –1. Table 5.6 gives the threshold values. Figure 5.1b shows the neural network with connection weights and threshold values.
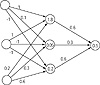
Figure 5.1b Neural Network for Cube Example
| Layer | Neuron | Threshold Value |
|---|---|---|
| hidden | 1 | 1.8 |
| hidden | 2 | 0.05 |
| hidden | 3 | -0.2 |
| output | 1 | 0.5 |
| Previous | Table of Contents | Next |