C++ Neural Networks and Fuzzy Logic by Valluru B. Rao M&T Books, IDG Books Worldwide, Inc. ISBN: 1558515526   Pub Date: 06/01/95

Backpropagation

The Backpropagation training algorithm for training feed-forward networks was developed by Paul Werbos, and later by Parker, and Rummelhart and McClelland. This type of network configuration is the most common in use, due to its ease of training. It is estimated that over 80% of all neural network projects in development use backpropagation. In backpropagation, there are two phases in its learning cycle, one to propagate the input pattern through the network and the other to adapt the output, by changing the weights in the network. It is the error signals that are backpropagated in the network operation to the hidden layer(s). The portion of the error signal that a hidden-layer neuron receives in this process is an estimate of the contribution of a particular neuron to the output error. Adjusting on this basis the weights of the connections, the squared error, or some other metric, is reduced in each cycle and finally minimized, if possible.

Figure for Backpropagation Network

You will find in Figure 7.1 in Chapter 7, the layout of the nodes that represent the neurons in a feedforward Backpropagation network and the connections between them. For now, you try your hand at drawing this layout based on the following description, and compare your drawing with Figure 7.1. There are three fields of neurons. The connections are forward and are from each neuron in a layer to every neuron in the next layer. There are no lateral or recurrent connections. Labels on connections indicate weights. Keep in mind that the number of neurons is not necessarily the same in different layers, and this fact should be evident in the notation for the weights.

Bidirectional Associative Memory

Bidirectional Associative Memory, (BAM), and other models described in this section were developed by Bart Kosko. BAM is a network with feedback connections from the output layer to the input layer. It associates a member of the set of input patterns with a member of the set of output patterns that is the closest, and thus it does heteroassociation. The patterns can be with binary or bipolar values. If all possible input patterns are known, the matrix of connection weights can be determined as the sum of matrices obtained by taking the matrix product of an input vector (as a column vector) with its transpose (written as a row vector).

The pattern obtained from the output layer in one cycle of operation is fed back at the input layer at the start of the next cycle. The process continues until the network stabilizes on all the input patterns. The stable state so achieved is described as resonance, a concept used in the Adaptive Resonance Theory.

You will find in Figure 8.1 in Chapter 8, the layout of the nodes that represent the neurons in a BAM network and the connections between them. There are two fields of neurons. The network is fully connected with feedback connections and forward connections. There are no lateral or recurrent connections.

Fuzzy Associative memories are similar to Bidirectional Associative memories, except that association is established between fuzzy patterns. Chapter 9 deals with Fuzzy Associative memories.

Temporal Associative Memory

Another type of associative memory is temporal associative memory. Amari, a pioneer in the field of neural networks, constructed a Temporal Associative Memory model that has feedback connections between the input and output layers. The forte of this model is that it can store and retrieve spatiotemporal patterns. An example of a spatiotemporal pattern is a waveform of a speech segment.

Brain-State-in-a-Box

Introduced by James Anderson and others, this network differs from the single-layer fully connected Hopfield network in that Brain-State-in-a-Box uses what we call recurrent connections as well. Each neuron has a connection to itself. With target patterns available, a modified Hebbian learning rule is used. The adjustment to a connection weight is proportional to the product of the desired output and the error in the computed output. You will see more on Hebbian learning in Chapter 6. This network is adept at noise tolerance, and it can accomplish pattern completion. Figure 5.7 shows a Brain-State-in-a-Box network.

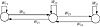
Figure 5.7  A Brain-State-in-a-Box, network.

What’s in a Name?

More like what’s in the box? Suppose you find the following: there is a square box and its corners are the locations for an entity to be. The entity is not at one of the corners, but is at some point inside the box. The next position for the entity is determined by working out the change in each coordinate of the position, according to a weight matrix, and a squashing function. This process is repeated until the entity settles down at some position. The choice of the weight matrix is such that when the entity reaches a corner of the square box, its position is stable and no more movement takes place. You would perhaps guess that the entity finally settles at the corner nearest to the initial position of it within the box. It is said that this kind of an example is the reason for the name Brain-State-in-a-Box for the model. Its forte is that it represents linear transformations. Some type of association of patterns can be achieved with this model. If an incomplete pattern is associated with a completed pattern, it would be an example of autoassociation.

Counterpropagation

This is a neural network model developed by Robert Hecht-Nielsen, that has one or two additional layers between the input and output layers. If it is one, the middle layer is a Grossberg layer with a bunch of outstars. In the other case, a Kohonen layer, or a self-organizing layer, follows the input layer, and in turn is followed by a Grossberg layer of outstars. The model has the distinction of considerably reducing training time. With this model, you gain a tool that works like a look-up table.