
by Valluru B. Rao
M&T Books, IDG Books Worldwide, Inc.
ISBN: 1558515526 Pub Date: 06/01/95

|
C++ Neural Networks and Fuzzy Logic
by Valluru B. Rao M&T Books, IDG Books Worldwide, Inc. ISBN: 1558515526 Pub Date: 06/01/95 |
| Previous | Table of Contents | Next |
The feedforward backpropagation network is a very popular model in neural networks. It does not have feedback connections, but errors are backpropagated during training. Least mean squared error is used. Many applications can be formulated for using a feedforward backpropagation network, and the methodology has been a model for most multilayer neural networks. Errors in the output determine measures of hidden layer output errors, which are used as a basis for adjustment of connection weights between the input and hidden layers. Adjusting the two sets of weights between the pairs of layers and recalculating the outputs is an iterative process that is carried on until the errors fall below a tolerance level. Learning rate parameters scale the adjustments to weights. A momentum parameter can also be used in scaling the adjustments from a previous iteration and adding to the adjustments in the current iteration.
The feedforward backpropagation network maps the input vectors to output vectors. Pairs of input and output vectors are chosen to train the network first. Once training is completed, the weights are set and the network can be used to find outputs for new inputs. The dimension of the input vector determines the number of neurons in the input layer, and the number of neurons in the output layer is determined by the dimension of the outputs. If there are k neurons in the input layer and m neurons in the output layer, then this network can make a mapping from k-dimensional space to an m-dimensional space. Of course, what that mapping is depends on what pair of patterns or vectors are used as exemplars to train the network, which determine the network weights. Once trained, the network gives you the image of a new input vector under this mapping. Knowing what mapping you want the feedforward backpropagation network to be trained for implies the dimensions of the input space and the output space, so that you can determine the numbers of neurons to have in the input and output layers.
The architecture of a feedforward backpropagation network is shown in Figure 7.1. While there can be many hidden layers, we will illustrate this network with only one hidden layer. Also, the number of neurons in the input layer and that in the output layer are determined by the dimensions of the input and output patterns, respectively. It is not easy to determine how many neurons are needed for the hidden layer. In order to avoid cluttering the figure, we will show the layout in Figure 7.1 with five input neurons, three neurons in the hidden layer, and four output neurons, with a few representative connections.
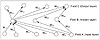
Figure 7.1 Layout of a feedforward backpropagation network.
The network has three fields of neurons: one for input neurons, one for hidden processing elements, and one for the output neurons. As already stated, connections are for feed forward activity. There are connections from every neuron in field A to every one in field B, and, in turn, from every neuron in field B to every neuron in field C. Thus, there are two sets of weights, those figuring in the activations of hidden layer neurons, and those that help determine the output neuron activations. In training, all of these weights are adjusted by considering what can be called a cost function in terms of the error in the computed output pattern and the desired output pattern.
The feedforward backpropagation network undergoes supervised training, with a finite number of pattern pairs consisting of an input pattern and a desired or target output pattern. An input pattern is presented at the input layer. The neurons here pass the pattern activations to the next layer neurons, which are in a hidden layer. The outputs of the hidden layer neurons are obtained by using perhaps a bias, and also a threshold function with the activations determined by the weights and the inputs. These hidden layer outputs become inputs to the output neurons, which process the inputs using an optional bias and a threshold function. The final output of the network is determined by the activations from the output layer.
The computed pattern and the input pattern are compared, a function of this error for each component of the pattern is determined, and adjustment to weights of connections between the hidden layer and the output layer is computed. A similar computation, still based on the error in the output, is made for the connection weights between the input and hidden layers. The procedure is repeated with each pattern pair assigned for training the network. Each pass through all the training patterns is called a cycle or an epoch. The process is then repeated as many cycles as needed until the error is within a prescribed tolerance.
There can be more than one learning rate parameter used in training in a feedforward backpropagation network. You can use one with each set of weights between consecutive layers.
| Previous | Table of Contents | Next |